Correct surface definitions | ||
| ||
- Continuous surfaces
Surfaces used with the general contact algorithm can span multiple unattached bodies. More than two surface facets can share a common edge. In contrast, all surfaces used with the contact pair algorithm must be continuous and simply connected. The continuity requirement has the following implications for what constitutes a valid or invalid surface definition for the contact pair algorithm:
In two dimensions the surface must be either a simple, nonintersecting curve with two terminal ends or a closed loop. Figure 1 shows examples of valid and invalid two-dimensional surfaces.
Figure 1. Valid and invalid two-dimensional surfaces for the contact pair algorithm.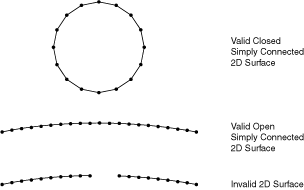
In three dimensions an edge of an element face belonging to a valid surface may be either on the perimeter of the surface or shared by one other face. Two element faces forming a contact surface cannot be joined just at a shared node; they must be joined across a common element edge. An element edge cannot be shared by more than two surface facets. Figure 2 illustrates valid and invalid three-dimensional surfaces.
Figure 2. Valid and invalid three-dimensional surfaces for the contact pair algorithm.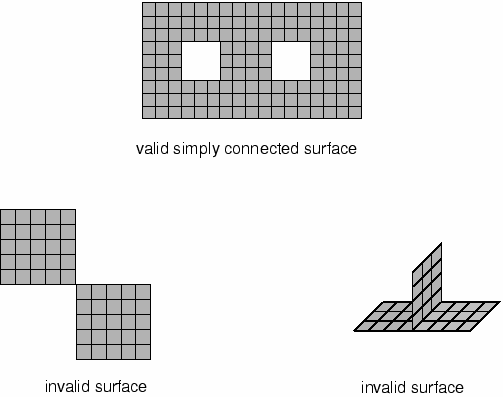
In addition, it is possible to define three-dimensional, double-sided surfaces. In this case both sides of a shell, membrane, or rigid element are included in the same surface definition, as shown in Figure 3.
Figure 3. Valid double-sided surface.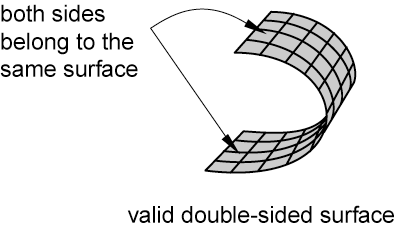
- Extending surfaces
Abaqus/Explicit does not extend surfaces automatically beyond the perimeter of the surface defined by the user. If a node from one surface is in contact with another surface and it slides along the surface until it reaches an edge, it may fall off the edge. Such behavior can be particularly troublesome because the node may later reenter from the back side of the surface, thereby violating the kinematic constraint and causing large jumps in acceleration at that node. Consequently, it is good modeling practice to extend surfaces somewhat beyond the regions that will actually contact. In general, we recommend covering each contacting body entirely with surfaces; the additional computational expense is minimal.
Figure 4 shows two simple box-like bodies constructed of brick elements.
Figure 4. Surface perimeters.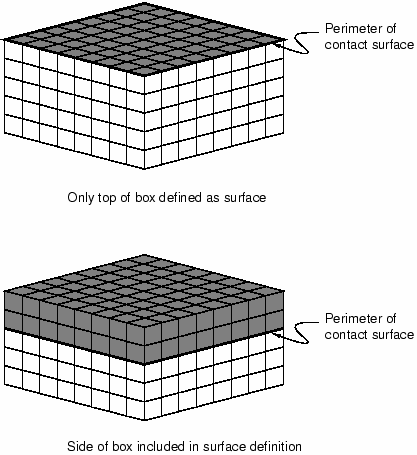
The upper box has a contact surface defined only on the top face of the box. While it is a permissible surface definition in Abaqus/Explicit, the lack of extensions beyond the raw edge could be problematic. In the lower box the surface wraps some distance around the side walls, thereby extending beyond the flat, upper surface. If contact is to occur only at the top face of the box, this extended surface definition minimizes contact problems by keeping any contacting nodes from going behind the contact surface.
- Mesh seams
Two nodes with the same coordinates (double nodes) can generate a seam or crack in a valid surface that appears to be continuous, as shown in Figure 5. A node sliding along the surface can fall through this crack and slide behind the contact surface. A large, nonphysical acceleration correction may be caused once penetration is detected. Surfaces defined in Abaqus/CAE will never have two nodes located at the same coordinates; however, imported meshes can have double nodes. Mesh seams can be detected in the Visualization module by drawing the free edges of the model. Any seams that are not part of the desired perimeter can be double-noded regions.
Figure 5. Example of a double-noded mesh.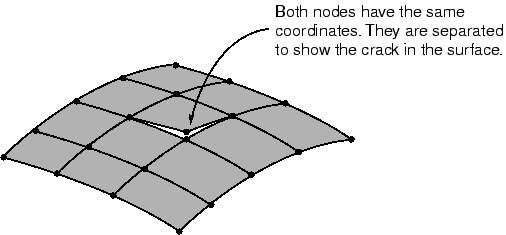
- Complete surface definition
Figure 6 illustrates a two-dimensional model of a simple connection between two parts. The contact definition shown in the figure is not adequate for modeling this connection because the surfaces do not represent a complete description of the geometry of the bodies. At the beginning of the analysis some of the nodes on surface 3 find that they are behind surfaces 1 and 2. Figure 7 shows an adequate surface definition for this connection. The surfaces are continuous and describe the entire geometry of the contacting bodies.
Figure 6. Example of an incorrect surface definition.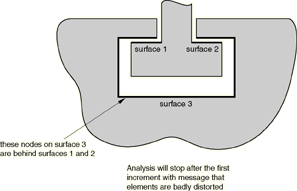 Figure 7. Correct surface definition.
Figure 7. Correct surface definition.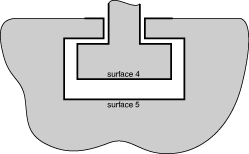
- Highly warped surfaces
No special treatment of warped surfaces is required for the general contact algorithm. However, when a surface used with the contact pair algorithm contains highly warped facets, a more expensive tracking approach must be used than the approach required when the surface does not contain highly warped facets. To keep the solution as efficient as possible, Abaqus monitors the warpage of the surfaces and issues a warning if surfaces become too warped; if the normal directions of adjacent facets differ by more than 20°, Abaqus issues a warning message. Once a surface is deemed to be highly warped, Abaqus switches from the more efficient contact search approach to a more accurate search approach to account for the difficulties posed by the highly warped surface.
For purposes of efficiency Abaqus does not check for highly warped surfaces every increment. Rigid surfaces are checked for high warpage only at the start of the step, since rigid surfaces do not change shape during the analysis. Deformable surfaces are checked for high warpage every 20 increments by default; however, some analyses may have surfaces with rapidly increasing warpage, making the default 20 increment frequency check inadequate. The frequency of warping checks can be changed to the desired number of increments. Some analyses in which the surface warping is less than 20° may also require the more accurate contact search approach associated with highly warped surfaces. The angle that defines high warpage can be redefined.
- Rigid element discretization
Complex rigid surface geometries can be modeled using rigid elements. Rigid elements in Abaqus/Explicit are not smoothed; they remain faceted exactly as defined by the user. The advantage of unsmoothed surfaces is that the surface defined by the user is exactly the same as the surface used by Abaqus; the disadvantage is that faceted surfaces require much higher mesh refinement to define smooth bodies accurately. In general, using a large number of rigid elements to define a rigid surface does not increase the CPU costs significantly. However, a large number of rigid elements does increase the memory overhead significantly.
The user must ensure that the discretization of any curved geometry on rigid bodies is adequate. If the rigid body discretization is too coarse, contacting nodes on the deformable body may snag, leading to erroneous results, as illustrated in Figure 8.
Figure 8. Potential effect of coarse rigid body discretization.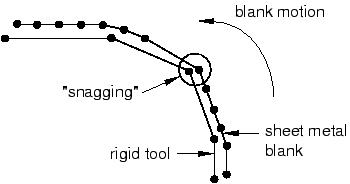
A node that is snagged on a sharp corner may be trapped from further sliding along the rigid surface for some time. Once enough energy is released to slide beyond the sharp corner, the node will snap dynamically before contacting the adjacent facet. Such motions cause noisy solutions. The more refined the rigid surface, the smoother the motion of the contacting slave nodes. The general contact algorithm includes some numerical rounding of features that prevents snagging of nodes from becoming a concern for discrete rigid surfaces. In addition, penalty enforcement of the contact constraints reduces the tendency for snagging to occur. Analytical rigid surfaces should normally be used with the contact pair algorithm for rigid bodies whose shape is an extruded profile or a surface of revolution.