Choosing the remeshing rule sizing method

You can allow Abaqus/CAE to choose a default sizing method based on the error indicator output variable, or you can specify a sizing method that will be used for all error indicators in the remeshing rule. If you specify the sizing method, you can also specify the adaptivity goal. For more information, see Solution-based mesh sizing.

Related Topics
Understanding adaptivity processes
Understanding adaptive remeshing
Creating a remeshing rule
In Other Guides
Solution-based mesh sizing
About adaptive remeshing

  1. From the Create Remeshing Rule dialog box, click the Sizing Method tab.

  2. Click the arrow to the right of the Method field, and select one of the following mesh size algorithms:

    • Choose Default method and parameters to allow Abaqus/CAE to choose the default calculation method for each error indicator output variable. By default, all of the error indicators except for element energy (ENDENERI) and heat flux (HFLERI) use the Minimum/maximum control mesh sizing algorithm. ENDENERI and HFLERI use the Uniform error distribution algorithm. The default error target is Automatic target reduction with a moderate mesh bias.

    • Choose the Uniform error distribution mesh sizing algorithm to force Abaqus/CAE to apply a sizing method that attempts to meet the specified error target in every element in the model. In most cases this approach leads to a globally converging mesh.

    • Choose the Minimum/maximum control mesh sizing algorithm to control the mesh density at the location of the minimum and maximum values of the base solution.

    For more information, see Solution-based mesh sizing.

  3. If you selected Uniform error distribution, specify the approach that Abaqus/CAE will use to determine the error indicator target:

    • Choose Automatic target reduction to allow Abaqus/CAE to generate successive mesh refinements that attempt to reduce the solution error by a fixed amount from the prior job in the adaptivity process. You select the maximum number of mesh iterations while creating an adaptivity process in the Job module. If you select Automatic target reduction, Abaqus/CAE will consider the rule to be satisfied when the error indicator reaches 1%. The criterion of 1% is intended only to provide protection against excessively expensive analysis jobs. In most cases Abaqus/CAE will complete all of the remesh iterations that you specified when you created the adaptivity process in the Job module.

    • Choose Fixed target, and enter the percentage error target. Abaqus/CAE uses this value to apply a sizing method that attempts to meet the error target in every element in the model. Such an approach ensures a globally converging mesh. Abaqus/CAE will consider the rule to be satisfied when the error indicator reaches the error indicator target.

  4. If you selected Minimum/maximum control, do the following from the Error Indicator Targets region:

    1. Specify the approach that Abaqus/CAE will use to determine the error target:

      • Choose Automatic target reduction to generate successive mesh refinements that attempt to reduce the solution error by a fixed amount from the prior analysis. You select the maximum number of mesh iterations in the Job module. If you select Automatic target reduction, Abaqus/CAE will consider the rule to be satisfied when the error indicator reaches 1%. The criterion of 1% is intended only to provide protection against excessively expensive analysis jobs. In most cases Abaqus/CAE will complete all of the remesh iterations that you specified when you created the adaptivity process in the Job module.

      • Choose Fixed targets, and enter the percentage error indicator targets at the location of the maximum and minimum value of the base solution. Abaqus/CAE uses these values to apply a heterogeneous sizing method that attempts to meet both targets at their respective locations. Abaqus/CAE will consider the rule to be satisfied when the error indicator corresponding to the maximum value of the base solution is reached. In addition, both error targets help Abaqus/CAE ensure that mesh refinement is focused on areas of interest. Conversely, they also help Abaqus/CAE ensure that disproportionate refinement is not applied to areas where the values of the base solution results are low.

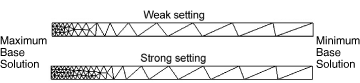
    2. Specify the Mesh Bias. The mesh bias further tunes the distribution of sizing between the locations of the maximum and minimum base solutions. When you choose Strong, the sizing method acts more aggressively and focuses more elements near locations of high base solution intensity. When you choose Weak, the sizing method acts less aggressively and generates fewer elements near locations of high base solution intensity. Figure 1 illustrates the effect of the bias factor.

      Figure 1. The impact of the bias factor on element size distribution.