ALE adaptive meshing and remapping in Abaqus/Standard

Original configuration projection is the default in Abaqus/Standard and determines the weight function from a least squares minimization procedure that minimizes node displacement in a projection of the mesh back to the original configuration. This method of smoothing affects only deformations of the mesh and not the original mesh.

Volume smoothing determines the weight function by computing a volume-weighted average of the element centers in the elements surrounding the node. In Figure 1 the new position of node M is determined by a volume-weighted average of the positions of the element centers, C, of the four surrounding elements. The volume weighting will tend to push the node away from element center C1 and toward element center C3, thus reducing element distortion.

Figure 1. Relocation of a node during a mesh sweep.

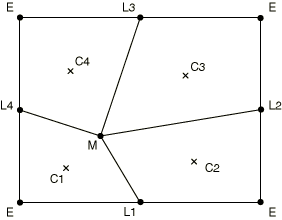
Volume smoothing is supported in structured domains, where every node is surrounded by four elements in two dimensions or eight elements in three dimensions.

The default smoothing method in Abaqus/Standard is original configuration projection. To choose an alternate smoothing method or to combine the smoothing methods, you specify the weighting factor for each method. When more than one smoothing method is used, a node is relocated by computing a weighted average of the locations predicted by each chosen method. All weights must be zero or positive, and their sum must be nonzero. The weights are significant only in a relative sense; their values are normalized so that their sum is 1.0.

ADAPTIVE MESH CONTROLS, NAME=name
original configuration projection weight, volume smoothing weight

ADAPTIVE MESH CONTROLS, NAME=name
0.5, 0.5

Step module: OtherALE Adaptive Mesh ControlsCreate: Name: name, Original configuration projection: original configuration projection weight, Volumetric: volume smoothing weight

The conventional forms of the basic smoothing methods may not perform well in highly distorted domains. You can use geometrically enhanced forms of the basic smoothing algorithms as a technique to mitigate distortion. These forms are heuristic and based on nodal locations only. Due to their heuristic nature, geometric enhancements may not always improve the mesh smoothing.

ADAPTIVE MESH CONTROLS, NAME=name, 
GEOMETRIC ENHANCEMENT=YES

Step module: OtherALE Adaptive Mesh ControlsCreate: Name: name, toggle on Use enhanced algorithm based on evolving element geometry

The mesh smoothing process begins with the mesh in its current displaced equilibrium configuration. Nodes that have no displacement degrees of freedom, such as those connected to acoustic elements, are maintained at their most recent configuration. Mesh smoothing is then driven by distortions in the current configuration and by boundary constraints. These boundary constraints can be described directly through adaptive mesh constraints. In the case of structural-acoustic boundaries the structural mesh boundary provides a constraint that controls the smoothing of adjacent acoustic element regions.

When these boundary constraints are much larger than the characteristic element length in the adaptive mesh domain, significant geometric changes, such as the development of corners, can occur. To prevent such changes, the constraints are applied gradually over a series of “sub-increments” onto the domain boundary. The number of sub-increments used is determined on the basis of the magnitude of the maximum surface displacement and the characteristic element dimension.

The remaining nodes (nodes not driven by constraints) are identified as interior nodes, free surface nodes, edge nodes, or corner nodes. These nodes are treated as described in Defining ALE adaptive mesh domains in Abaqus/Standard.

At the end of mesh sweeping the new geometry is checked to ensure that elements did not become severely distorted during mesh smoothing. Abaqus/Standard responds to severe distortion in different ways, depending on the elements and procedures used. When adaptive meshing is used with acoustic elements, the current analysis increment is repeated with a reduced time increment, followed by another adaptive mesh smoothing attempt. When adaptive meshing is used with other elements, severe distortion results in abandonment of mesh smoothing for that increment. In cases where adaptive mesh constraints are also defined, Abaqus/Standard aborts since the constraints cannot be satisfied.

In most cases the frequency of adaptive meshing is the parameter that most affects the mesh quality. By default, mesh smoothing will be performed after each converged structural analysis increment. You can change the frequency of adaptive meshing, except when adaptive mesh constraints are defined.

ADAPTIVE MESH, FREQUENCY=number of increments

Step module: OtherALE Adaptive Mesh DomainEdit: toggle on Use the adaptive mesh domain below, Frequency: number of increments

The adaptive mesh smoothing equations are solved explicitly by sweeping iteratively over the adaptive mesh domain. During each mesh sweep, nodes in the domain are relocated based on the current positions of neighboring nodes to reduce element distortion.

Mesh smoothing is performed following the end of a converged increment. You can control the intensity of the mesh smoothing by defining the number of mesh sweeps required. When the displacements are large, more iterations are usually required. When used in acoustic analyses, more iterations are usually required when the volume of the elements in the acoustic domain decreases compared to the case when the volume increases during structural loading.

You can specify the number of mesh sweeps to be performed in each adaptive mesh increment. The default number of mesh sweeps is one.

By applying the mesh sweeping algorithm repeatedly, the mesh will converge; in other words, nodal positions are obtained that do not change with further mesh sweeping. However, it is usually not necessary to apply mesh smoothing until a converged mesh is obtained; the main objective is to reduce element distortion.

ADAPTIVE MESH, MESH SWEEPS=number of sweeps

Step module: OtherALE Adaptive Mesh DomainEdit: toggle on Use the adaptive mesh domain below, Remeshing sweeps per increment: number of sweeps

To ensure that the results are output only for the configuration that satisfies equilibrium, Abaqus/Standard always outputs the results at the end of the Lagrangian phase. The Eulerian phase that follows the Lagrangian phase will leave the structure out of equilibrium for the next increment. This sequence has a consequence that after the last Eulerian phase is carried out at the end of the step, equilibrium will not be satisfied exactly at the beginning of the next step and the solution at the end of the step will differ slightly from the solution at the zero increment of the following step. Equilibrium can again be established by following the step that had adaptive meshing by a step that removes all the adaptive mesh domains and allows the structure to equilibrate. A one-increment step will usually suffice. This is particularly important when the following step is a perturbation procedure that uses the solution from the previous step as the base state.

Frequency steps that follow adaptive mesh steps will also be impacted, because element mass is not advected during mesh smoothing. This impact on the element mass can be significant, depending on the extent of adaptive mesh motion and change in element size due to mesh smoothing. Abaqus will provide a warning message in cases where adaptive meshing precedes a frequency step; you should evaluate the impact of your updated mesh configuration when interpreting results from a frequency step in these cases.