A Brief Explanation of NVH Theory

Theoretical Background of Structural NVH Simulations

To explain the concept of structural NVH an idealization of an automotive vehicle is explained below. The chassis and tires are considered and the vibrations from driving on a road are analyzed.

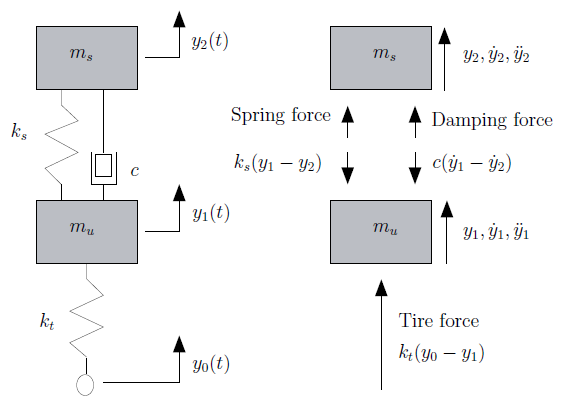The image above shows an automotive modeled as a simple system of masses, springs and dashpots. The dashpot is used to provide damping and has a damping coefficient C. The two springs represent the stiffness of the tires and the suspension. The masses represent the mass of the tires and the chassis. A free body force representation is made where the displacements, velocity and accelerations of each mass are also considered. Then the equations of motion for this system are written as follows:

$m_{u} {\ddot{y}}_{1} - k_{t} (y_{0} - y_{1}) + k_{s} (y_{1} - y_{2}) + c ({\dot{y}}_{1 -} {\dot{y}}_{2}) = 0,$

$m_{s} {\ddot{y}}_{2} - k_{s} (y_{1} - y_{2}) - c ({\dot{y}}_{1 -} {\dot{y}}_{2}) = 0.$

A matrix representation of the considered system of differential equations reads :

$M \ddot{y} + C \dot{y} + K y = F$

$\Leftrightarrow [\begin{matrix} m_{u} & 0 \\ 0 & m_{s} \end{matrix}] [\begin{matrix} {\ddot{y}}_{1} \\ {\ddot{y}}_{2} \end{matrix}] + [\begin{matrix} c & - c \\ - c & c \end{matrix}] [\begin{matrix} {\dot{y}}_{1} \\ {\dot{y}}_{2} \end{matrix}] + [\begin{matrix} (k_{t} + k_{s}) & - k_{s} \\ - k_{s} & k_{s} \end{matrix}] [\begin{matrix} y_{1} \\ y_{2} \end{matrix}] = [\begin{matrix} {\begin{matrix} k \end{matrix}}_{t} y_{0} \\ 0 \end{matrix}]$

The right side of these equations represents the enforced load which is time dependent. In case of harmonic loads these differential equations can be transformed to a system of linear equations. Solving this system for a range of load frequencies provides the corresponding amplitudes of displacements. Such a procedure is called frequency response analysis. In case that the right side of the above equation is not a harmonic one it can be transformed by means of Fourier transform and then analyzed.

Theoretical Background of Structural-Acoustic NVH Simulation

The governing equations for free time-harmonic vibrations in a solid-acoustic region are given as:

Solid:	$σ_{i j, j} + f_{i} + ρ_{s} ü_{i} = 0$	$x \in Ω_{s}$
Solid coupling:	$σ_{i j} n_{j}^{s} = p n_{i}^{a}$	$x \in Γ$
Acoustic:	$▵ p + q \frac{1}{c^{2}} \ddot{p} = 0$	$x \in Ω_{α}$
Acoustic coupling:	$▿ p n_{i}^{a} = ρ_{a} ü_{i} n_{j}^{a}$	$x \in Γ$

Quantities which appear here are :

$s$	solid domain
$a$	acoustic domain
$Γ$	interface between two domains
$u_{i}$	displacements
$p$	pressure
$σ_{i j}$	stress tensor of the solid domain
$n_{j}^{s}$	outward pointing normal to the solid domain
$n_{i}^{a}$	outward pointing normal to the acoustic domain
$i, j$	=1,2,3
$ρ_{s}$	density of the solid
$ρ_{a}$	density of the acoustic media
$c$	speed of sound in the acoustic media
$f_{i}$	loading on the solid
$q$	loading on the acoustic media

We assume that structural stresses are given by a linear stress-strain constitutive modeling and the acoustic domain pressure has a linear relation to the volumetric strain. Additionally assume that the loading on the solid and acoustic domains is harmonic and the solution to be steady-state time-harmonic. Thus, the following two harmonic functions ,

$u_{t} = u_{A} e^{i Ω t}$ and $P_{t} = P_{A} e^{i Ω t}$

are a solution to the problem defined above. Quantities which appear here are,

$Ω$	excitation frequency
$u_{A}$	amplitude for the structural domain
$p_{A}$	amplitude for the acoustic domain

Discretization of the above equations in context of finite element method leads to,

$- Ω^{2} [\begin{matrix} {\begin{matrix} M \end{matrix}}_{s} & 0 \\ {\begin{matrix} A \end{matrix}}^{T} & {\begin{matrix} M \end{matrix}}_{a} \end{matrix}] [\begin{matrix} u_{A} \\ P_{a} \end{matrix}] + i Ω [\begin{matrix} C_{s} & 0 \\ 0 & C_{a} \end{matrix}] [\begin{matrix} u_{A} \\ P_{a} \end{matrix}] + [\begin{matrix} K_{s} & - A \\ 0 & K_{a} \end{matrix}] [\begin{matrix} u_{A} \\ P_{a} \end{matrix}] = [\begin{matrix} P_{s} \\ P_{a} \end{matrix}]$

with the following quantities:

$M$	mass matrix
$C$	damping matrix
$K$	stiffness matrix
$P_{s}$	applied harmonic structural force
$P_{a}$	applied harmonic acoustic pressure
$A$	coupling matrix which models the interface between acoustic domain and structural components

This system of equations is solved for each excitation frequency providing the corresponding amplitudes of displacements and pressure. This procedure again corresponds to the frequency response analysis but now with the possibility to compute the acoustic pressure.

Possible Applications of NVH Simulation in Engineering

Most applications of NVH are found in the automotive or aerospace fields. NVH analyses can be carried out for both performance and comfort reasons. For example modal analyses on cars are carried out in order to prevent resonation of the engine and chassis frequencies. An acoustic analysis for example could be performed to ensure cabin comfort. Apart from engineering reasons, NVH analyses may be carried out when designing sound systems, or to predict noise levels around industrial sites or airports etc.

The applications of NVH are:

Engine noise vibration testing.
Acoustic performance testing.
Sound power testing.
Environmental noise measurements and noise field mapping.
Structural dynamics and vibration testing.
Occupational health and safety.