Sizing Optimization for Circular Beams | ||
| ||
Supported Finite Element Features for Circular Beams
The circular beam type based upon the Timoshenko beam element formulation is supported for optimization. The corresponding element type definition is summarized in the following table for different solvers:
| Solver | Element type definition |
|---|---|
| Abaqus | *ELEMENT, TYPE=B31 |
| ANSYS® | ET, 1, 188 |
| Circular beam |
|---|
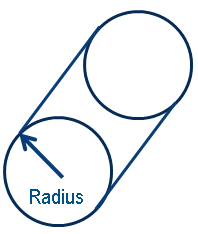 |
As shown in the above picture the radiuses of circular beams are supported as design variables. Thus, the following cross section property definition is supported for sizing optimization:
| Solver | Cross section definition |
|---|---|
| Abaqus | *BEAM SECTION, SECTION = CIRC |
| ANSYS® | SECTYPE,1,BEAM,CSOLID SECDATA,25., |
Note: Annular (pipe) type sections are not yet supported by SIMULIA Tosca Structure.
The radiuses of the circular beam sections can be optimized simultaneously with the elemental shell thicknesses. Outside of the design area any type of elements can be applied. However, in the design area only linear material behavior is allowed (i.e. plasticity or geometrical non-linearities are inadmissible). Contact and constant temperature loadings are supported in context of sizing optimization for circular beams. Also, both linear static and linear modal type analyzes are supported.
The main features and the corresponding comments are summarized in the following table:
| Features | Comment |
|---|---|
| Simultaneously usage of circular beams and shells | Supported |
| Contact | Supported, also for design elements |
| Constitutive non-linear modeling outside the design area | Supported |
| Constitutive non-linear materials in design area | Not supported |
| Temperature loading | Design independent temperature loading is supported |
| Geometrical non-linearities | Not supported |
| Linear static analysis | Supported |
| Linear modal analysis | Supported |
| Steady state dynamics | Supported |
![]()
Optimization Formulation Options for Circular Beams
All the existing design responses except stresses are supported for sizing optimization with circular beams and can be used for constraints and objective function definitions. All the symmetry constraints available in the sizing module can be applied simultaneously with variable bounds and clustering on design radiuses. The number of load cases is not limited. DRESPs from static, modal (eigenfrequency) and frequency response (also vibro acoustic) analyses are supported. All the mentioned features are summarized in the following table:
| Feature | Comment |
|---|---|
| DRESPs for static load cases | Supported, e.g. Stiffness, Displacements, Forces … |
| Multiple load cases | Supported, arbitrary number |
| DRESPs for modal eigenfrequency analysis | Supported, eigenfrequencies |
| DRESPs for frequency response analysis | Supported, also vibroacoustics |
| Mass | Supported |
| COG and Inertia | Supported |
| Symmetry constraints | Supported, various constraints |
| Variable bounds and clustering | Supported |
| DRESPs with stresses | Not supported |
![]()
Limitations
The limitations of sizing optimization for circular beams are as follows:
Note:
- Only Abaqus and ANSYS® solvers are supported.
- Material non-linearities within the design area and geometrical non-linearities are not supported.
-
Only circular beam section type is supported with radius as design variable:
Solver Cross section definition Abaqus *BEAM SECTION, SECTION = CIRC ANSYS® SECTYPE,1,BEAM,CSOLID SECDATA,25.,
-
Only the Timoshenko type beam element is supported:
Solver Element type definition Abaqus *ELEMENT, TYPE=B31 ANSYS® ET, 1, 188 - Design responses with stresses are not supported.
![]()
Introduction Example for Abaqus
Within this example the definition of a sizing optimization problem for circular beams is demonstrated. We consider the following model with the illustrated boundary conditions.
| Mechanical model |
|---|
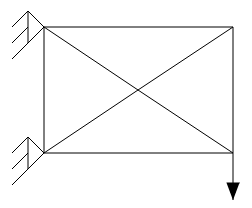 |
The model corresponds to a cantilever beam which consists of 8 elements. It is supported on the left nodes and loaded at the right bottom node.
The corresponding Abaqus input file is given below:
*Heading
** Job name: example Model name: Model-1
** Generated by: Abaqus/CAE 6.14-2
*Preprint, echo=NO, model=NO, history=NO, contact=NO
** PART INSTANCE: Part-1-1
*Node
1, -1., 0.600000024, 0.
2, 0., -0.100000001, 0.
3, 1., -0.800000012, 0.
4, -1., -0.800000012, 0.
5, 1., 0.600000024, 0.
*Element, type=B31
1, 1, 2
2, 2, 3
3, 4, 3
4, 4, 2
5, 2, 5
6, 5, 1
7, 1, 4
8, 3, 5
*Nset, nset=Part-1-1_Set-1, generate
1, 5, 1
*Elset, elset=Part-1-1_Set-1, generate
1, 8, 1
*Nset, nset=Part-1-1_Set-4, generate
1, 5, 1
*Elset, elset=Part-1-1_Set-4, generate
1, 8, 1
*Nset, nset=Part-1-1_Set-5, generate
1, 5, 1
*Elset, elset=Part-1-1_Set-5, generate
1, 8, 1
*Orientation, name=Part-1-1-Ori-1
1., 0., 0., 0., 1., 0.
1, 0.
** Section: Section-1 Profile: Profile-1
*Beam Section, elset=Part-1-1_Set-1, material=steel,
temperature=GRADIENTS, section=CIRC
0.1
0.,0.,1.
*System
*Nset, nset=Set-1
3,
*Nset, nset=Set-2
1, 4
*Nset, nset=Set-3
3, 5
*Nset, nset=_PickedSet7
3,
*Nset, nset=_PickedSet8
3,
** MATERIALS
*Material, name=steel
*Density
7850.,
*Elastic
2e+11, 0.33
** STEP: Step-1
*Step, name=Step-1, nlgeom=NO
*Static
1., 1., 1e-05, 1.
** BOUNDARY CONDITIONS
** Name: BC-1 Type: Symmetry/Antisymmetry/Encastre
*Boundary
Set-2, ENCASTRE
** LOADS
** Name: Load-1 Type: Concentrated force
*Cload
_PickedSet8, 2, 1e+06
** OUTPUT REQUESTS
*Restart, write, frequency=0
** FIELD OUTPUT: F-Output-1
*Output, field, variable=PRESELECT
** HISTORY OUTPUT: H-Output-1
*Output, history, variable=PRESELECT
*End Step
The corresponding SIMULIA Tosca Structure parameter file is given in the following.
For the present optimization we maximize the stiffness by minimizing the deflection and at the same time we keep the original mass of the structure. The original mass is enforced using a relative constraint of exactly one. The initial radiuses are equal to 0.1. The upper and lower bounds on the radiuses are set to 0.12 and 0.01.
FEM_INPUT
ID_NAME = example
FILE = example.inp
END_
DRESP
ID_NAME = Disp
LIST = NO_LIST
DEF_TYPE = SYSTEM
TYPE = DISP_ABS
ND_GROUP = _PickedSet7
GROUP_OPER = MAX
LC_SET = ALL, 1, ALL, MAX
END_
DRESP
ID_NAME = Mass
LIST = NO_LIST
DEF_TYPE = SYSTEM
TYPE = WEIGHT
EL_GROUP = ALL_ELEMENTS
GROUP_OPER = SUM
END_
DV_SIZING
ID_NAME = Task-1_DESIGN_AREA_
EL_GROUP = ALL_ELEMENTS
END_
DVCON_SIZING
ID_NAME = MY_DVCON_SIZING
CHECK_TYPE = THICKNESS_BOUNDS
EL_GROUP = ALL_ELEMENTS
LOWER_BOUND = 0.01
UPPER_BOUND = 0.12
MAGNITUDE = ABS
END_
OBJ_FUNC
ID_NAME = Minimize_Disp
DRESP = Disp, 1.
TARGET = MIN
END_
CONSTRAINT
ID_NAME = Wieght_100
DRESP = Mass
MAGNITUDE = REL
LE_VALUE = 1
END_
OPTIMIZE
ID_NAME = Task-1
DV = Task-1_DESIGN_AREA_
OBJ_FUNC = Minimize_Disp
CONSTRAINT = Wieght_100
STRATEGY = SIZING_SENSITIVITY
DVCON = MY_DVCON_SIZING
END_
EXIT
The optimization results are shown in the following figures. As one can recognize the displacement value of the right bottom node is decreased and the structural volume corresponds to its initial value. The upper and lower bounds of design variables are not violated.
| Optimization history | Optimized radiuses | Thickness |
|---|---|---|
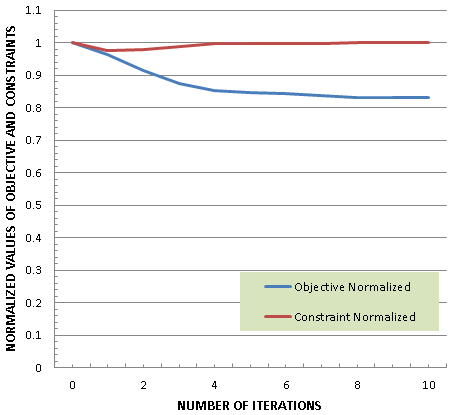 |
 |
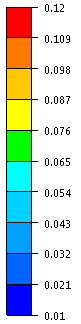 |
![]()
Introduction Example for ANSYS®
Within this example the definition of a sizing optimization problem for circular beams is demonstrated. In particular there is only one beam with one fixed node (left on the picture) and fixed moment of inertia. Additionally there is a force applied on the other node along Z direction.
| Mechanical model |
|---|
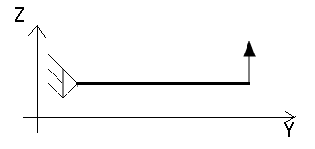 |
The corresponding ANSYS® input file is given below:
! Model name: thick_beam.cdb
/PREP7
/NOPR
LOCAL,R5.0,LOC,11,0,-45.,-17.8483,11.7365
LOCAL,R5.0,ANG,11,0,0.,-90.,0.
LOCAL,R5.0,PRM,11,0,1.,1.
CSYS,11
N,230857,0.,9.98750019,100.
N,230858,0.,9.98649979,0.
CSYS,0
MP,EX,1,10.
MP,PRXY,1,0.3
MP,DENS,1,7.85E-9
ET,1,188
SECNUM,1
SECTYPE,1,BEAM,CSOLID,Beam Section,0
SECOFFSET,SHRC,,,,,,
SECDATA,25.,,,,,,,,,
EBLOCK,19,SOLID
(19i8)
1 1 0 1 0 0 0 0 2 0 1274067 230857 230858
-1
D,230857,ALL,0.,0.
/SOLU
!
! L O A D - S T E P S
!Anonymous Ansys Step 1
!
TIME,1.
!
F,230858,FZ,50.,0.
solve
FINISH
The corresponding SIMULIA Tosca Structure parameter file is given below. For the present optimization we maximize the stiffness by minimizing the deflection. The initial radius is equal to 25.0 units.
FEM_INPUT
ID_NAME = MY_INPUT_FILES
FILE = thick_beam.cdb, ansys
END_
DRESP
ID_NAME = DRESP_DISP
DEF_TYPE = SYSTEM
TYPE = DISP_ABS
NODE = 230858
CS_REF = CS_0
END_
DRESP
ID_NAME = DRESP_VOL
DEF_TYPE = SYSTEM
TYPE = WEIGHT
EL_GROUP = ALL_ELEMENTS
END_
OBJ_FUNC
ID_NAME = MY_OBJ_FUNC
TARGET = MIN
DRESP = DRESP_VOL, ,
END_
CONSTRAINT
ID_NAME = CONSTRAINT_DISP
MAGNITUDE = ABS
DRESP = DRESP_DISP
LE_VALUE = 0.9
END_
DV_SIZING
ID_NAME = DESIGN_AREA
EL_GROUP = ALL_ELEMENTS
END_
OPTIMIZE
ID_NAME = OPTIMIZE_1_SIZING_OPTIMIZATION
DV = DESIGN_AREA
OBJ_FUNC = MY_OBJ_FUNC
CONSTRAINT = CONSTRAINT_DISP
STRATEGY = SIZING
END_
STOP
ID_NAME = GLOBAL_STOP_CONDITION_1
ITER_MAX = 50
END_
Result: The output of the optimization shows that the radius of the beam is now thicker with 5 more units (R = 30).
![]()
Optimization Example: Combined Optimization of Outer Shell Elemental Thicknesses and Elemental Radiuses of Inner Ground Structure
We consider the following model with the illustrated boundary conditions, pictured initial deformation and the corresponding initial stress.
| Mechanical model | Deformation | Stress |
|---|---|---|
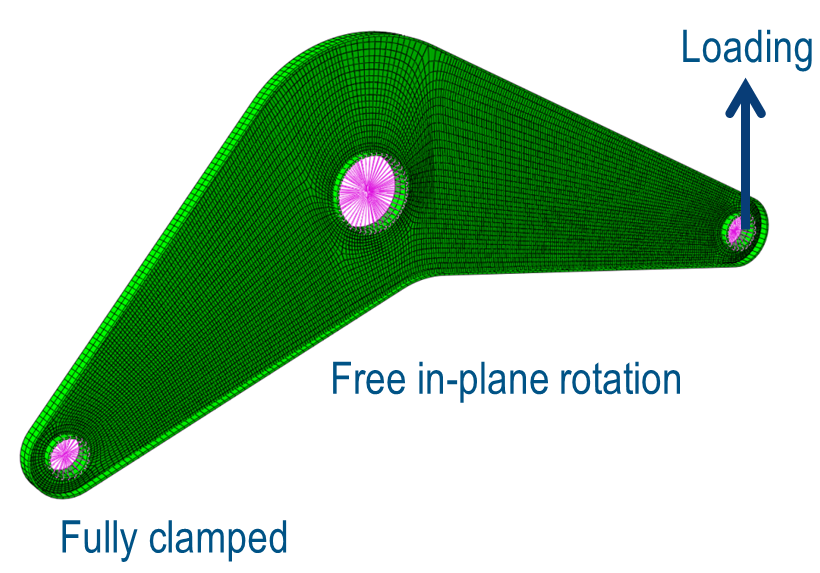 |
 |
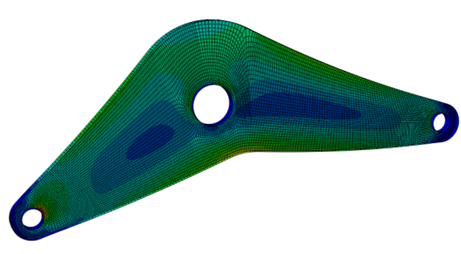 |
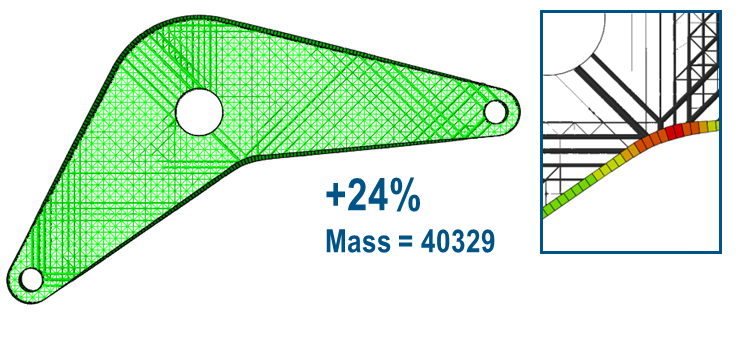
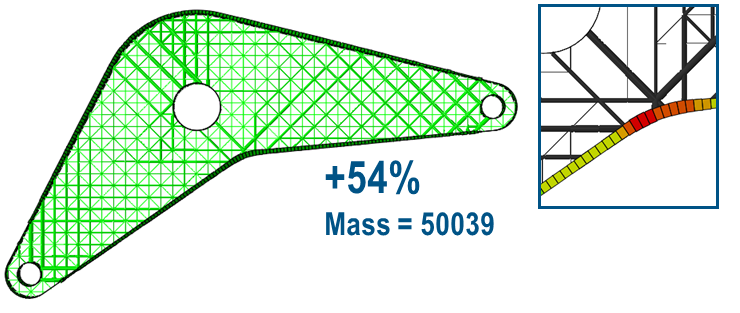
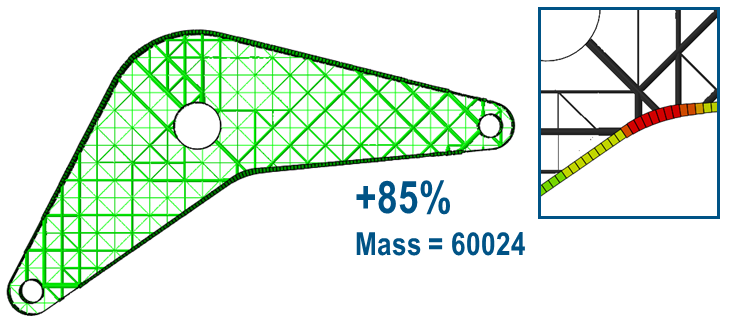
The structural mass is to be minimized kipping the displacement at loading point less than 0.6mm. The inner structure is consisting of either shell thicknesses or lattice build of circular beams. Then ones optimized either the inner shell thicknesses or the radiuses of the lattice simultaneously with the elemental thicknesses of the other shell reinforcements.
The optimization results are shown in the following figure:
| Thickness | Free continuous shell thickness | Triangular fine lattice |
|---|---|---|
 |
 |
 |
| Thickness | Triangular medium lattice | Triangular coarser lattice |
 |
 |
 |
![]()
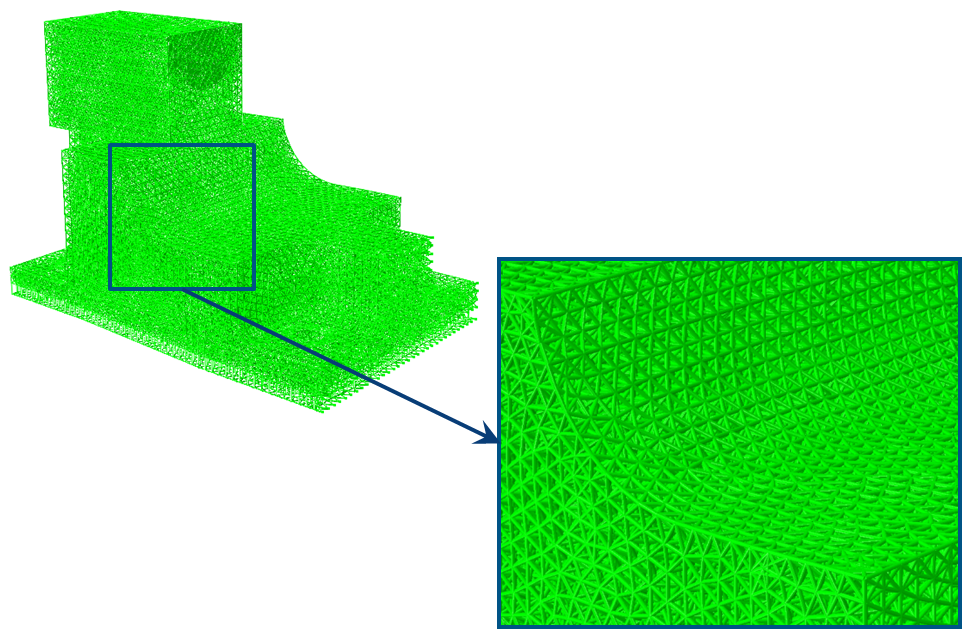
Optimization Example: Lattice Optimization of Door Stop.
We consider the following model.
 |
Optimization Objectives:
- Maximize stiffness
- Keep the original structural mass
- Displacement for interface constraints
Radius of circular beam element:
- Initial: 0.18
- Lower bound: 0.00001 (approximates void)
- Upper bound: 0.7 (289%)
The following figure represents the section cuts for the original structure having uniform radius sections for the entire structure:
 |
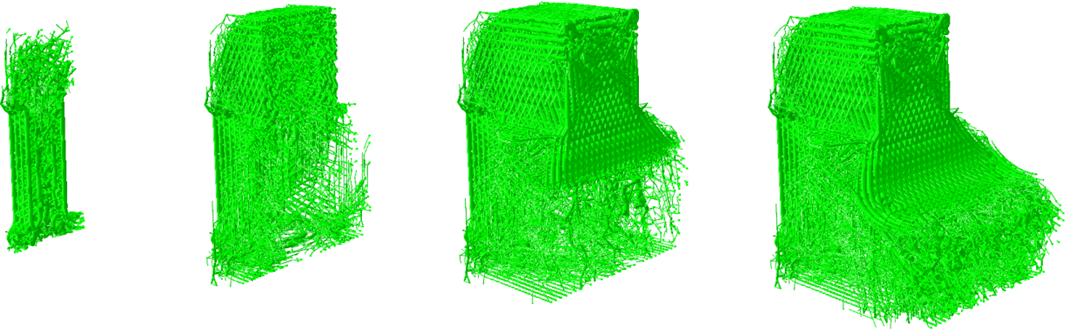
The next figure shows the radius distribution of the section cuts for the optimized structure:
 |
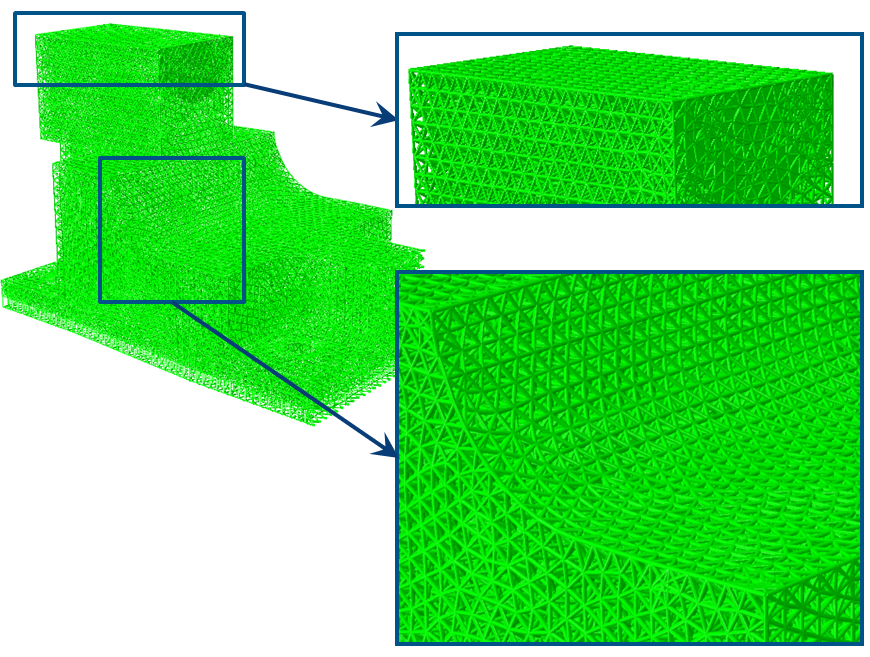
Some enlarged details of the initial and the optimized structures are pictured in the following figure:
| Initial radiuses | Optimized radiuses |
|---|---|
 |
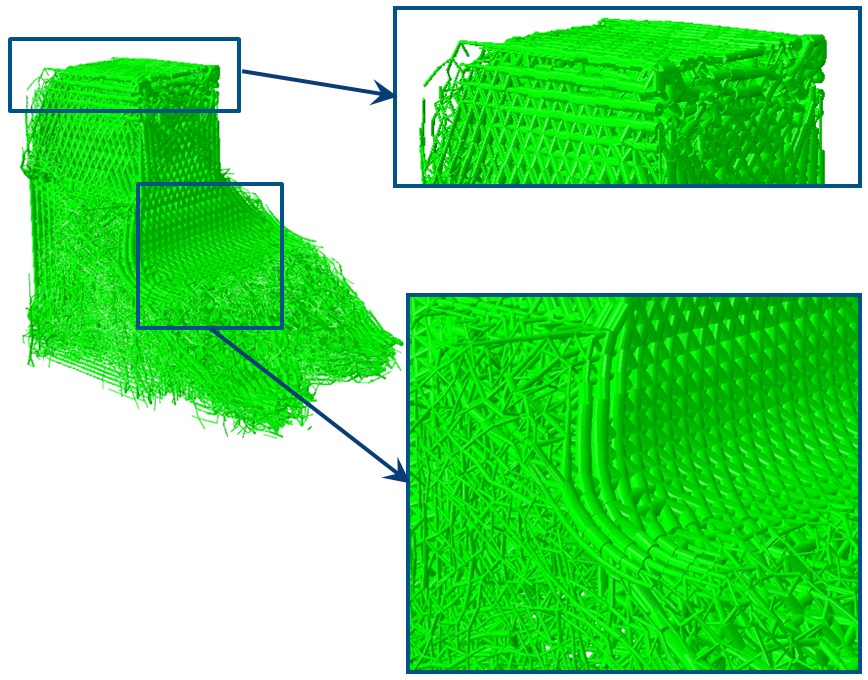 |
The following figures show the optimization iteration history for the design responses being the stiffness energy measure for the objective and mass and displacement as constraints:
| Stiffness energy measure | Mass (normalized) | Displacement interface constraints |
|---|---|---|
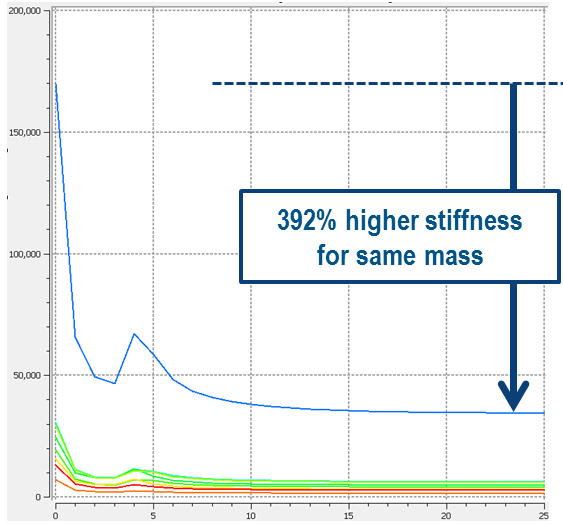 |
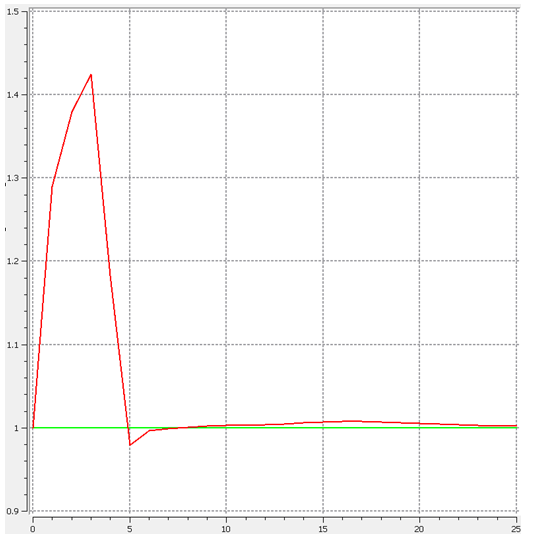 |
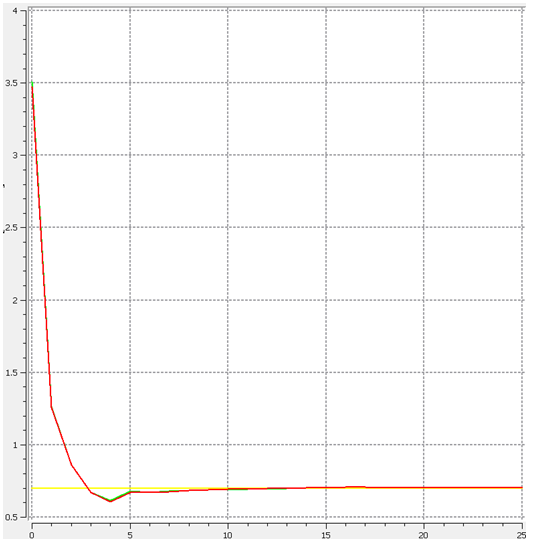 |