Special Remarks Using Sensitivity-Based Algorithm

Semi-analytical sensitivity calculation

The sensitivity-based algorithm uses semi-analytical sensitivities based on a finite difference of the stiffness and mass element matrices:

$\frac{\partial K}{\partial x}\approx \Delta K^{*}=\Delta K+{\alpha }^{jk}\text{ with }\Delta K=\frac{K_{0+p}-K_0}{\Delta x}$

Where K is the stiffness matrix, $K_0$ is the original matrix and $K_{0+p}$ is the perturbed matrix when one of the nodes is moved. The first term in the above equation is necessary to calculate the sensitivity for most of the design responses that are available in SIMULIA Tosca Structure.bead. To get this term we utilize a "matrix-step" (see figure below).

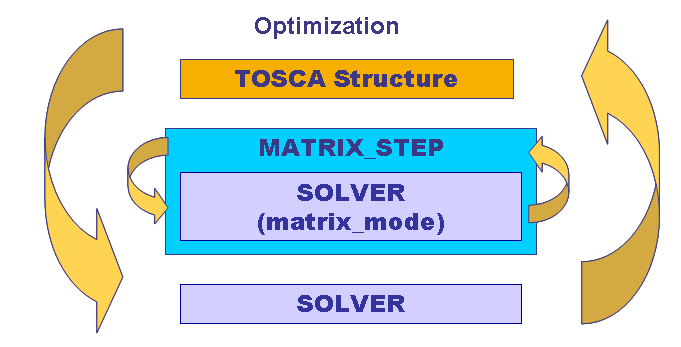This matrix step's only purpose is to perturb all design nodes to get these pertubed matrices - the original matrix is obtained in the last perturbation (PERTURBATION = 0) where also the results of the FE-problem is wanted.

To avoid too long optimization run times it is important to understand this workflow. It has two potential pitfalls which may slow the optimization tremendously:

1. Too long calculation during matrix steps
2. Too many pseudo loads

1. The first case is discussed in more detail in the chapters concerning the specific solvers. But in short, the problem is that some solvers have no possibility of only writing the element matrices without solving the whole system. The number of matrix steps usually varies between 4-8 which in worst case leads to 9 full solvers runs every iteration.
2. The second case is a mutual problem with almost every sensitivity-based optimization algorithm; using the adjoint method to calculate sensitivities one has to solve the adjoint problems. The adjoint problems are added as "pseudo loads" or extra load cases which are added to the original input deck. The number of these pseudo loads depends on the types of design responses and how they are defined.

It would demand a lengthy discussion to explain in detail exactly when and why which loads are added but some rules of thumb is given here:

• Compliance and eigenvalue optimization do not add pseudo loads (self adjoint problems) and are therefore preferable optimization quantities.
• Avoid the DRESPs without any direction (DISP_ABS, FS_DISP_ABS etc.). These design responses lead to three pseudo loads (in all 3 dimensions) whereas the single directional (DISP_X, DISP_X_ABS, FS_DISP_X_ABS, etc.) only lead to one pseudo load.
• Define the load case of interest directly in the DRESP definition using LC_SET. If only one load case is referenced SIMULIA Tosca Structure will only add one pseudo load. If LC_SET = ALL,ALL,ALL (which is default!) SIMULIA Tosca Structure will add a pseudo load for each load case found in the original input deck.