Weibull Distribution

The Weibull Distribution density function $f_{X} (x)$ is defined by

\begin{array}{l} f_{X} (x) & = \frac{β}{α} {(\frac{x - y}{α})}^{β - 1} \exp [- {(\frac{x - y}{α})}^{β}] & x \geq y \\ = 0 & otherwise \end{array}

where $α > 0$ is the scale parameter, $β > 0$ is the shape parameter, and $γ (- \infty < γ < \infty)$ is the location parameter.

The Weibull probability distribution function is

F_{X} (x) = 1 - \exp [- {(\frac{x - y}{α})}^{β}] x \geq y .

If $γ = 0$ , as is true for many cases, the density function reduces to the following:

\begin{array}{l} f_{X} (x) & = \frac{β}{α} {(\frac{x}{α})}^{β - 1} \exp [- {(\frac{x}{α})}^{β}] & x \geq 0 \\ = 0 & otherwise \end{array}

and the probability distribution function is

F_{X} (x) = 1 - \exp [- {(\frac{x}{α})}^{β}] x \geq 0.

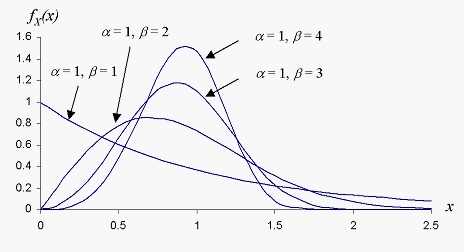
The reduced density function, called a two-parameter Weibull distribution, is used in probabilistic fracture mechanics and fatigue. The two-parameter Weibull distribution is implemented in Isight.

The mean value and standard deviation of the random variable $X$ with the two-parameter Weibull distribution are given as follows:

μ_{X} = α Γ (1 + \frac{1}{β})

and

σ_{X} = α {Γ (1 + \frac{2}{β}) - {[Γ (1 + \frac{1}{β})]}^{2}}^{\frac{1}{2}}

where $Γ$ is the well known gamma function

Γ (k) = \int_{0}^{\infty} e^{- u} u^{k - 1} d u

$Γ (k) = (k - 1)!$ when $k$ is an positive integer.

The Weibull distribution can take different shapes, as shown in the following figure. For example, this distribution is often used to describe the life of capacitors and ball bearings.