Skewed Normal Distribution

The skewed normal distribution is defined by three parameters (Owen, 1956):

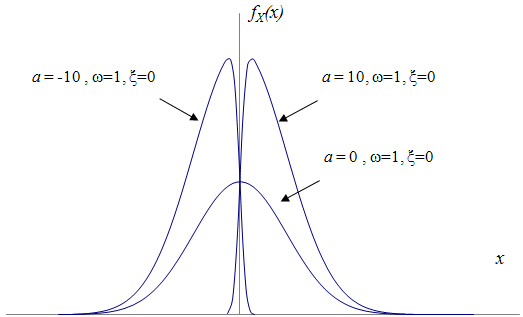
A normal distribution is obtained when the skewness is zero (i.e., ). The direction in which the distribution is skewed depends on the sign of .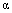

The skewed normal cumulative distribution function is

F_{X} (x) = Φ (\frac{x - ξ}{ω}) - 2 T (\frac{x - ξ}{ω}, α),

where $T (h, a)$ is the Owen’s T-function,

T (h, a) = \frac{1}{2 π} \int_{0}^{a} \frac{e^{- \frac{1}{2} h^{2} (1 + x^{2})}}{1 + x^{2}} d x .

The mean and standard deviations for the skewed normal distribution are

\begin{array}{l} μ_{x} = ξ + (\sqrt{\frac{2}{π}}) \frac{ω α}{\sqrt{1 + α^{2}}} \\ σ_{x} = ω \sqrt{(1 - \frac{2 α^{2}}{(1 + α^{2}) π})} \end{array} .

The skewed normal probability density function, as shown in the following figure,

f_{X} (x) = \frac{1}{ω π} e^{- \frac{{(x - ξ)}^{2}}{2 ω^{2}}} \int_{- \infty}^{α (\frac{x - ξ}{ω})} e^{- \frac{t^{2}}{2}} d t = 2 ϕ (\frac{x - ξ}{ω}) Φ (α \frac{x - ξ}{ω}),

where $ϕ (\cdot)$ is the standard normal probability density function and $Φ (.)$ is the standard normal cumulative distribution function.