Simple Importance Sampling

In other words, the mean value of this new sampling density function is the MPP, whereas the variance is the same as the original density function. If $Φ (μ, σ, x)$ is the standard normal probability density function, where $μ$ is the mean and $σ^{2}$ is the variance, then the probability density function of the sample set is $Φ (M P P, σ, x)$ while that of the original problem is $Φ (M V P, σ, x)$ .

Simple importance sampling estimates the probability as follows (Man-Suk, 1989):

P_{f} = \frac{1}{N} \sum_{i = 1}^{N} I (X_{i}) φ (M V P, σ, X_{i}) = \frac{1}{N} \sum_{i = 1}^{N} \frac{I (Y_{i}) φ (M V P, σ, Y_{i})}{φ (M P P, σ, Y_{i})},

where $x_{i}$ are $N$ samples drawn around the MVP, $Y_{i}$ are $N$ samples drawn around the MPP, and $I (X o r Y)$ I(X or Y) is an indicator function such that

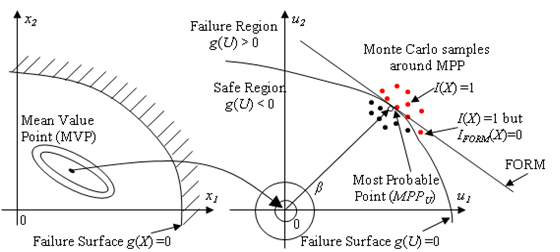
I (X) = {\begin{matrix} 1 & g (X) < 0 \\ 0 & g (X) \geq 0 \end{matrix}

FORM uses a linear approximation of the constraint surface (see the figure above) to compute the probability of failure as

$P f, F O R M = Φ (- β)$ ,

where $Φ$ is the standard normal distribution function and $β$ is the distance to the MPP in U-space. If the failure function is nonlinear or the random variables are not normally distributed, the FORM estimate can be corrected using importance sampling as followed (Man Mok, 2003):

P_{f} = P_{f, F O R M} + \sum_{i = 1}^{N} \frac{(I (Y_{i}) - I_{F O R M} (Y_{i})) φ (M V P, σ, Y_{i})}{φ (M P P, σ, Y_{i})},

where $I_{F O R M} (Y)$ is the indicator function of the linear approximation used by FORM defined as

I_{F O R M} (X) = {\begin{matrix} 1 & T (Y) \cdot {M P P}_{U} > β \\ 0 & otherwise \end{matrix}

where ${M P P}_{u}$ is the MPP in U-space.

The probability of failure obtained by correcting the FORM estimate is more accurate than that obtained using simple importance sampling only when the following conditions are satisfied:

the constraint is nearly linear,
the MPP search converges to a point on the constraint, and
the number of samples is very low.