Pointer Control Algorithm | ||
| ||
The following figure illustrates the control algorithm.
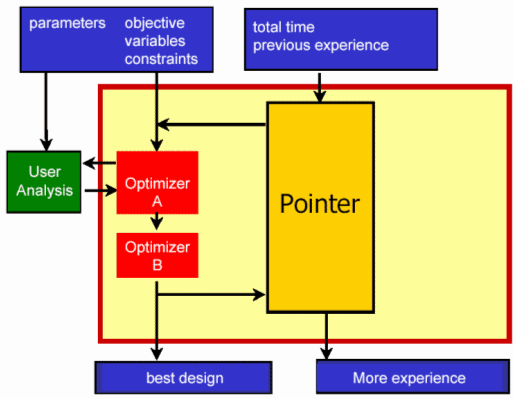
The Pointer technique consists of a complementary set of optimization algorithms. Currently, the Pointer technique uses linear simplex, sequential quadratic programming (SQP), downhill simplex, and genetic algorithms. All have control parameters (such as initial step sizes) that need to be set properly to operate efficiently. This process, illustrated in the above figure, is called optimizer training. The inputs to the process are the design variables, constraints, and the search objective, with the total time available for the search and any previous experience in terms of the selection and right settings of the optimizers.
The Pointer control algorithm varies the optimizer settings in such a way that either:
- The best answer is found in the shortest time. In this case the optimizers are configured such that the maximum rate of improvement of the objective function is achieved from a single starting position.
- The most experience is gained. The optimizer settings are selected in such a way that the highest optimizer robustness is achieved for a given optimization time. The robustness is defined as the mean harmonic error of the best objective function (ever found) normalized by the local optimum for a set of random starting vectors. This approach is an order of magnitude slower than merely finding the best answer, but the experience gained will allow you to solve similar classes of problems in the shortest possible time.
Usually, it is not possible to identify the problem topology in such a way that you can select the proper algorithms and settings. A real-life example is shown in the following figure. The topology is that of the drag of an airfoil computed by Computational Fluid Dynamics (CFD) as a function of its shape. Previously, the user (from experience) assumed that the drag was a smooth function of the geometry. From the starting point, a small step was selected to calculate the gradients accurately. Because the topology of the drag had surface waves, the steepest downhill slope was considered to be along this wave. If you had picked a larger step size, you would have concluded that the direction normal to the waves has the “relevant” steepest downhill slope.
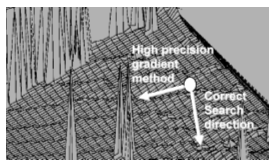
The waves are not caused by the physics of the problem (drag), but by numeric interference of converging loops inside the numeric code that calculates the drag. Almost all simulation codes that use partial differential equations exhibit such behavior. The spikes in this plot represent code-failures, another difficult topological feature not inherent in real physics.
A dozen approaches were identified to correct pathological topologies and find the correct relevant search direction. These pathological topologies are created by the type of numeric algorithm used in the simulation code, not by the specific design problem the simulation code addresses. Therefore, the solution that the Pointer technique presents is valid over a wide range of topologies.