Pointer's Performance on Benchmark Problems

However, any optimization problem can usually be solved when the right answer is already known and the starting point "tweaked." This comparison will focus on the added value of the Pointer technique versus the already good set of core algorithms.

Although many problems have been solved with the Pointer technique, this section uses a truss optimization problem because it represents a typical design problem in mechanical or aerospace engineering. The following figure shows a truss as it supports a series of point loads.

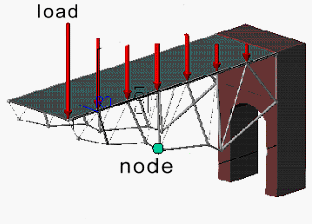
The bridge is supported at the right edge and free at the left edge. It has six joints whose positions are chosen by the optimizer so as to minimize the weight or cost subject to a given set of loads. The weight is computed by determining the minimum bar dimensions that can support the applied load.

The problem is hard because, as the joints locations move with respect to each other, the loads on the bars change from compression to tension and back. A bar under compression has to be much thicker (thin-walled cylinder) than a bar under tension (wire). The weight of the truss structure is a discontinuous function of the locations of the joints.

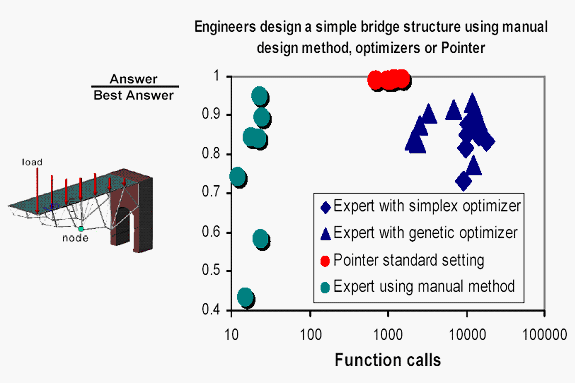
The optimization task was to minimize the weight of the truss in 30 minutes. In 1993, Mathias Hadenfeld completed the task of optimizing the truss from a random starting point. Hadenfeld was an expert user of optimization. He was free to tweak and restart the solution until he felt that no more progress could be made, but he could not change the starting point. His results are shown in the graph below (blue symbols). On average he had more success with the genetic algorithm than the downhill simplex method, and the gradient method failed. On average his answers were 15% away from the known optimum because of the difficult topology of the problem.

In 1999, the same problem was given to 13 groups of between 7 and 15 professional engineers. They were given the Pointer technique and its graphical user interface displaying the truss. They were asked to minimize the weight without using the optimization. They had to manually input the joint coordinates and run the analysis to see if an improvement was made. Because an analysis could be done in less than a second, 30 minutes was ample time to complete the task. The number of iterations was between 10 and 30. In our experience this also represents the average number of industrial product design iterations.

The groups of engineers came up with vastly different answers. Some were more than twice as heavy as the best solution. However, some came up with solutions that were within 5% of the right answer. It is interesting to note that they only achieved these results through the use of the graphical representation of the truss. In a subsequent test without the graphics, no engineer came within 20% of the optimizer's best answer.

Next, the Pointer technique was given the control over the core optimizers (red symbol in the graph). Just like the expert, the Pointer technique required less function calls to find the answer with genetic algorithm than with the downhill simplex algorithm. But with its standard settings, which allow the optimal use of all algorithms, the Pointer technique was able to consistently get the right answer from any starting point with just 1000 function calls (< 1 minute).

Even though the group of experts got different answers when solving the problem manually, all achieved the correct answer when using the Pointer technique under its standard settings.

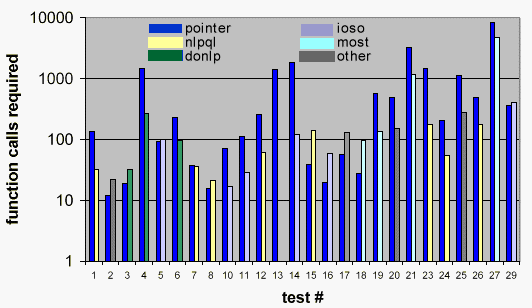
The Pointer technique was compared against a dozen high quality optimizers on standard benchmark tests. The test used was devised by Dr. Sandgren to represent a wide variety of hard optimization problems in all fields of mathematics and engineering. Though the problems are hard, they were typically not as hard as the ones experienced when working with clients.

The following graph shows the result of the test. Nevertheless, maybe not surprisingly, the Pointer technique performed exceedingly well on the test. It was the only code capable of solving all the problems. This is all the more impressive considering that the same standard settings were used for all the test cases and that there was no expert intervention in the process. In terms of speed it is usually comparable to the best codes for each of the specific problems. The "best" benchmark results were provided by Dr. Egorov the author of Indirect Optimization on the basis of Self-Organization (IOSO). Other codes in the comparison were IOSO, Sequential Quadratic Programming (NLPQL), DO NonLinear Programming (DONLP), and Multifunction Optimization System Tool (MOST).