Optimal Latin Hypercube Technique | ||||
|
| |||
In the Optimal Latin Hypercube technique the design space for each factor is divided uniformly (the same number of divisions, , for all factors). These levels are randomly combined to generate a random Latin Hypercube as the initial DOE design matrix with points (each level of a factor studies only once). An optimization process is applied to the initial random Latin Hypercube design matrix. By swapping the order of two factor levels in a column of the matrix, a new matrix is generated and the new overall spacing of points is evaluated. The goal of this optimization process is to design a matrix where the points are spread as evenly as possible within the design space defined by the lower and upper level of each factor.
Note: This type of matrix is not reproducible (unless the same random seed is reused) because the Optimal Latin Hypercube begins as a random Latin Hypercube and is optimized using a stochastic optimization process.
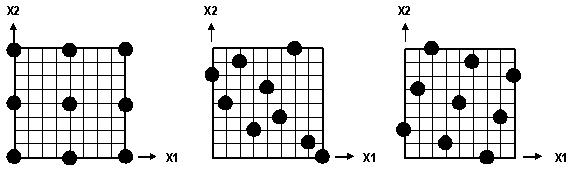
The Optimal Latin Hypercube concept is illustrated in the following figure for a configuration with two factors () and nine design points. In the first graph, a standard three level Orthogonal Array is shown. While this matrix has nine design points, there are only three levels for each factor. Consequently, a quadratic model could be fit to this data, but it is not possible to determine if the actual functional relationship between the response and these two factors is more nonlinear than quadratic. The second graph shows a random Latin Hypercube.This matrix also includes nine design points for the two factors, but there are nine levels for each factor as well, allowing higher-order polynomial models to be fit to the data and greater assessment of nonlinearity. However, the design points in the second graph are not spread evenly within the design space. For example, there is little data in the upper-right and lower-left corners of the design space. An Optimal Latin Hypercube matrix is displayed in the third graph. With this matrix, the nine design points cover nine levels of each factor and are spread evenly within the design space. For cases where one purpose of executing the design experiment is to fit an approximation to the resulting data, the Optimal Latin Hypercube gives the best opportunity to model the true function, or true behavior, of the response across the range of the factors.
A number of different optimality criteria can be used to achieve an even spread of points. Isight uses one widely used optimality criterion in this implementation: the criterion based on the maximin distance criterion. As described in (Jin et al., 2005):
A design is called a maximin distance design (Johnson et al., 1990) if it maximizes the minimum inter-site distance:
where , is the distance between two sample points and :
Morris and Mitchell (1995) proposed an intuitively appealing extension of the maximin distance criterion. For a given design, by sorting all the inter-sited distance , a distance list and an index list can be obtained, where ’s are distinct distance values with is the number of pairs of sites in the design separated by , and is the number of distinct distance values. A design is called a -optimal design if it minimizes:
where is a positive integer. With a very large , the criterion is equivalent to the maximin distance criterion.
The Optimal Latin Hypercube code implemented in Isight was developed by:
-
Professor Wei Chen, Northwestern University,
-
Dr. Ruichen Jin, Ford Motor Company (formerly a student of Professor Chen), and
-
Dr. Agus Sudjianto, formerly with Ford Motor Company.
There are two major advances of this algorithm, compared to other optimal design of experiments algorithms, which increase both the efficiency and robustness of the algorithm:
-
Development of an efficient global optimal search algorithm, “enhanced stochastic evolutionary (ESE) algorithm”
-
Efficient algorithms for evaluating optimality criteria (significant reduction in matrix calculations to evaluate new/modified designs during search)