Modified Method of Feasible Directions (MMFD) Technique

The Modified Method of Feasible Directions technique has the following features:

• rapidly obtains an optimum design,

• handles inequality and equality constraints, and

• satisfies constraints with high precision at the optimum.

The sequence of steps followed by the MMFD technique are as follows:

1. $q=0$, $\underline{x}={\underline{x}}^0$
2. $q=q+1$
3. Evaluate 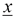$F$() and $g_j$(); $j=1,2,\dots ,M$
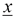4. Identify the set of critical constraints, $J$
5. Calculate $\nabla F\left(\underline{x}\right)\nabla g_j\left(\underline{x}\right),j\in J$
6. Determine the usable/feasible search directions, ${\underline{S}}^q$
7. Perform 1D search to find a*
8. Set ${\underline{x}}^q={\underline{x}}^{q-1}+a\times x{\underline{S}}^q$
9. Check for convergence; if not converged, go to Step 2.

The MMFD technique uses one of the following methods to find the search direction at each iteration q:

• If no constraints are active or violated, the (previously described) unconstrained Conjugate Gradient method is used.
• If any constraints are active and none are violated, the MMFD technique minimizes

$\nabla F\left({\underline{x}}^{q-1}\right)\times {\underline{S}}^q$

subject to: $\nabla g_j({\underline{x}}^{q-1})\times S^q\le 0;j\in J$

$S^q\times S^q\le 1$.

• If one or more constraints are violated, the MMFD technique

minimizes $\nabla F\left({\underline{x}}^{q-1}\right)\times {\underline{S}}^q-\mathrm{\Phi }\beta$

subject to: $\nabla g_j\left(x^{q-1}\right)\times S^q+{\mathrm{\Theta }}_j\beta \le 0;j\in J$

${\underline{S}}^q\times {\underline{S}}^q\le 1$

where

$J$ is the set of active and violated constraints

$\mathrm{\Phi }$

is a large positive number

is a push-off factor for constraints

= 0 for active constraints

> 0 for violated constraints

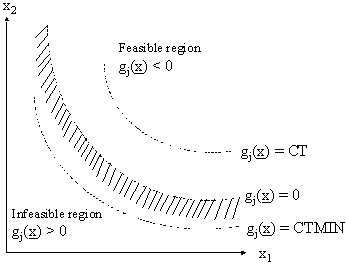
The active and violated constraints are identified as follows:

$g_j\left(\underline{x}\right)$ is active, if $\mathrm{C}\mathrm{T}\le g_j\left(\underline{x}\right)\le \mathrm{C}\mathrm{T}\mathrm{M}\mathrm{I}\mathrm{N}$

$g_j\left(\underline{x}\right)$ is violated, if $g_j\left(\underline{x}\right)>\mathrm{C}\mathrm{T}\mathrm{M}\mathrm{I}\mathrm{N}$

Active and Violated Constraint Identification