Lognormal Distribution

Given a random variable $X$ defined over $0 < x < \infty$ , and given that $Y = 1 n X$ is normally distributed with mean $μ_{Y}$ and standard deviation $σ_{Y}$ , the random variable $X$ follows the Lognormal distribution, defined by the probability density function.

The probability density function is

\begin{array}{l} f_{X} (x) & = \frac{1}{β x \sqrt{2 π}} \exp [- \frac{1}{2 β^{2}} {(\log x - α)}^{2}] & x > 0 \\ = 0 & otherwise . \end{array}

The lognormal distribution function is

F_{X} (x) = Φ (\frac{1 n x - α}{β})

Note that $α = μ_{Y}$ and $β = σ_{Y}$ . The mean and standard deviation of the random variable $X$ are given as follows:

μ_{X} = e^{(α + \frac{1}{2} β^{2})}

and

σ_{X} = \sqrt{μ_{X}^{2} (e^{β^{2}} - 1)} .

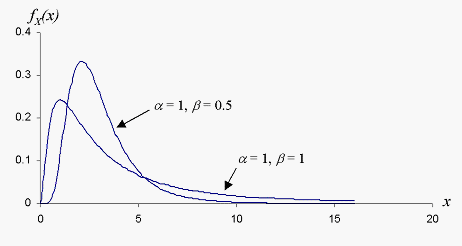
The lognormal probability density function, as shown in the following figure, is often used to describe material properties, sizes from a breakage process, and the life of some types of transistors.